jzoj503题解

原题链接

题目描述

• 1934年，东印度（今孟加拉国）学者森德拉姆（ $\texttt{Sandaram}$ ）发现了“正方形筛子”。

4	7	10	13	16	…
7	12	17	22	27	…
10	17	24	31	38	…
13	22	31	40	49	…
16	27	38	49	60	…
…	…	…	…	…	…

• 设在该方筛中第 $x$ 行第 $y$ 列的数字是 $a_{x,y}$ ，求 $\sum\limits^n_{i=1}\sum\limits^m_{j=1}{a_{i,j}}$ 的值 $\mod 2^{64}$。

解法一

• $n,m \le 8$。

随你咋搞，手算指数级乱搞都行。

预估得分 $10$ 分。

解法二

• $n,m \le 500$。

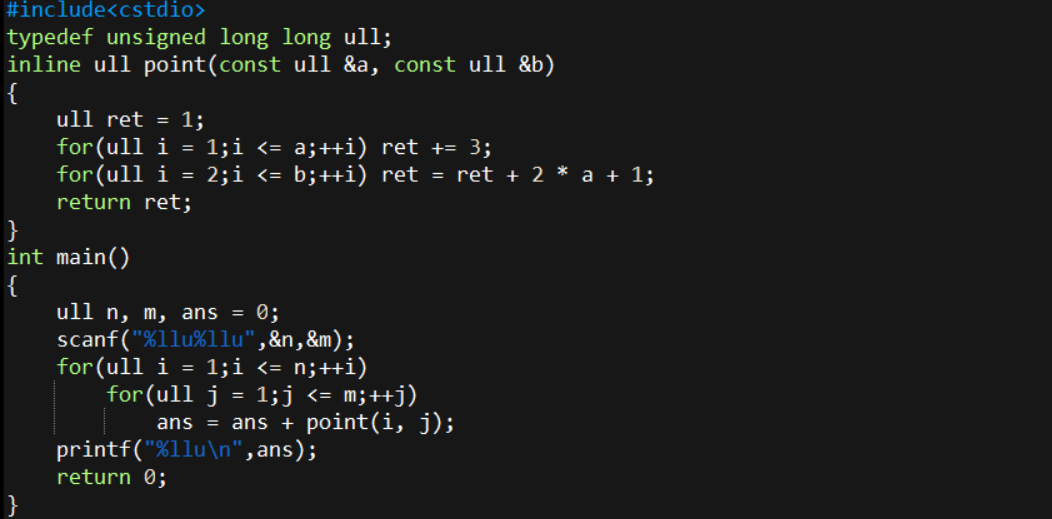
发现公差有规律，于是暴力计算每个数暴力加和。

时间复杂度 $\mathcal{O}(mn(m+n))$，预估得分 $30$ 分。

解法三

• $n,m \le 10^4$。

考虑求出每一个点的通项公式，求和。

通过观察和计算、化简，我们知道了：

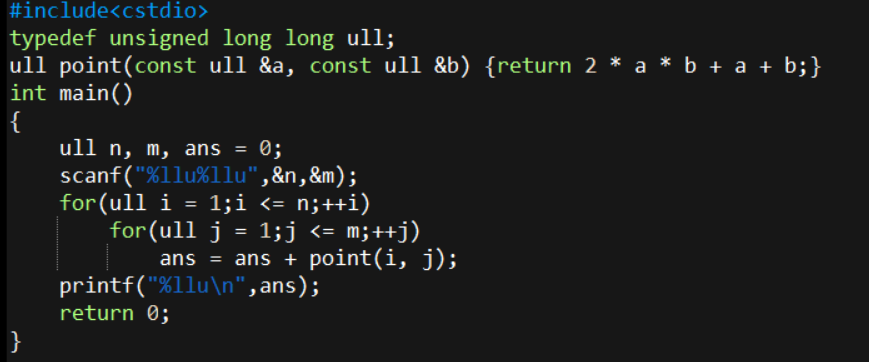
设一个点的坐标为 $x,y$，则这个点的数值为 $2 \times a \times b + a + b$，这样可以做到 $O(1)$ 知道每个点，暴力加。

时间复杂度 $\mathcal{O}(n \times m)$，预估得分 $50$ 分。

解法四

• $n,m \le 7 \times 10^7$。

考虑优化。

不难发现，每一行都是一个公差为 $2 \times 行数 +1$ 的等差数列，因此可以暴力算每一行或每一列。

然后我们可以取两个当中的最小值以加速。

暴力算每一行时间复杂度 $\mathcal{O}(n)$，暴力算每一列时间复杂度 $\mathcal{O}(m)$，取最小值时间复杂度 $\mathcal{O}(\min (n,m))$，应该都可以获得 $70$ 分。

解法五

• $1 \le n,m \le 6 \times 10^{16}$。

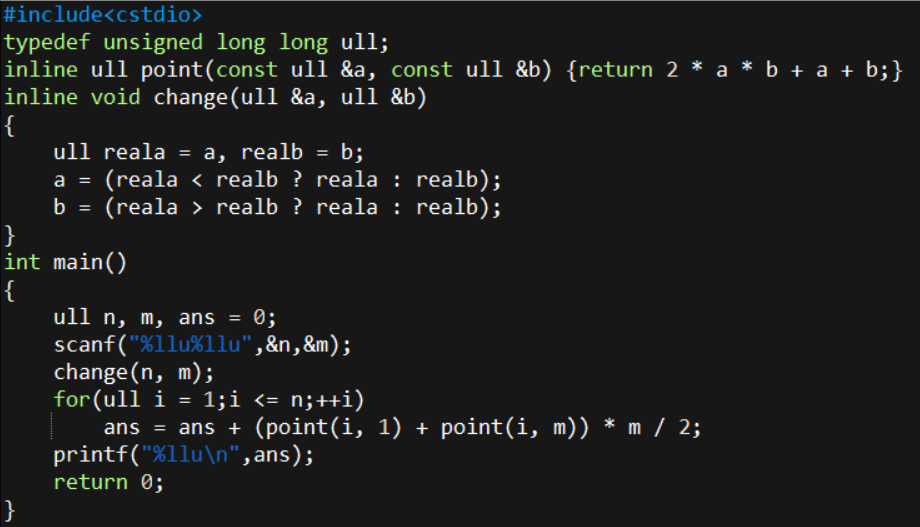
想出解法四的人不难发现其实每一列的和也是个等差数列，因此还是用等差数列公式，在$\mathcal{O}(1)$ 的复杂度内即可解决。

得分 $100$ 分。

---

放个代码：

cpp

#include<cstdio>
//其实这是一道愉快的数学题！
#define ___(_) ((_)+2)
#define ____(_) ((_)-1)
#define _____(_,__) ((_)*(__))
#define ______(_) ((_)/2)
#define _______ unsigned long long
int main()
{
	_______ _, __;
	scanf("%llu%llu",&_,&__);
	printf("%llu\n",______(_____(_,_____(__,____(_____(___(_),___(__)))))));
	return 0;
}

完结撒花！

难度：小学数学。